Last time we looked at the very foundation of electronics. Charge, E-fields, voltage, current, and conventional current. You’ll be happy to know that now we’re going to look a something a little more practical, circuit basics. Some of this topic may be review for you as well. Stick with me and we’ll get to the good stuff soon. Things you can actually use for your design efforts. But, this foundation stuff is useful in knowing what’s going on. Let’s dive in.
The Voltage Law: No Free Lunch
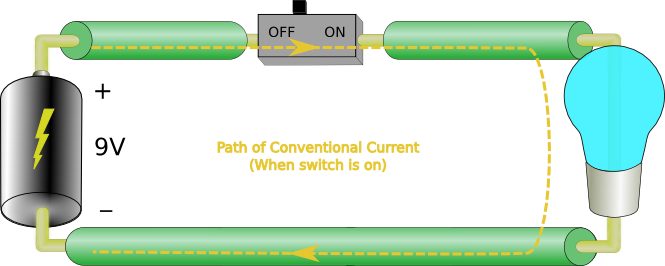
We’re gonna start off with something called Kirchoff’s voltage law. This, and Kirchoff’s current law, are the starting point for circuit theory. It’s a bit dry, but quite useful. Let’s look at our light bulb circuit again.
This time we’ve given the battery a voltage value, 9V. What does this mean? Well, if we start with our pretend positive charge, remember conventional current, it leaves the positive terminal and heads toward the negative terminal when the switch is closed. When it leaves the positive terminal it can be said to have 9V of energy. What happens as it travels around the circuit? It still has 9V of energy as it enters the light bulb, but as it goes through the bulb it loses those 9V of energy which then become heat and light. When it enters the negative terminal, our positive charge has 0V of energy. We can represent this as follows.
The battery is labeled with a + sign and a – sign and 9V between them. The light bulb is also labeled with a + and a – sign and 9V between them. Notice that the + battery terminal is connected to the + light terminal. What does that mean?
We know that the battery is an energy source and that the light is an energy sink. We call the battery a source or power rail and the lamp is called a load. So the ‘+ 9V –’ label of the battery tell us that the battery gives 9V of energy to the current carrierscariers, while the ‘+ 9V –’ label of the load tells us that the load takes 9V of energy from the current carriers. In circuit design we say that the voltage drop across the lamp is 9V. So when the battery supplies 9V of energy to the current carriers, the load takes that energy away from them. Notice how the load takes away the exact amount of energy supplied by the source. This is basically Kirchoff’s voltage law. More formally it states:
The sum of all voltage sources in a circuit = the sum of all voltage drops in that circuit.
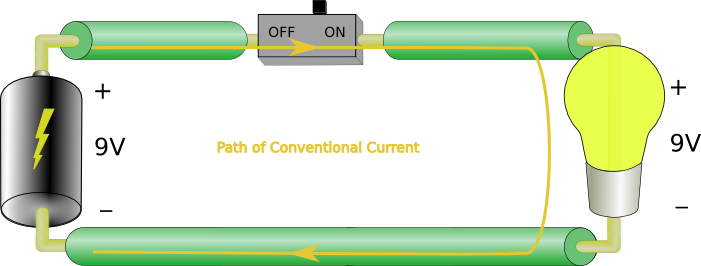
Here’s another example.
In this case we have two lamps and our 9V battery. In this case you see that each lamp only drops 4.5V of energy. So the sum of the voltage drops (4.5V +4.5V) is equal to the sum of all the sources, 9V.
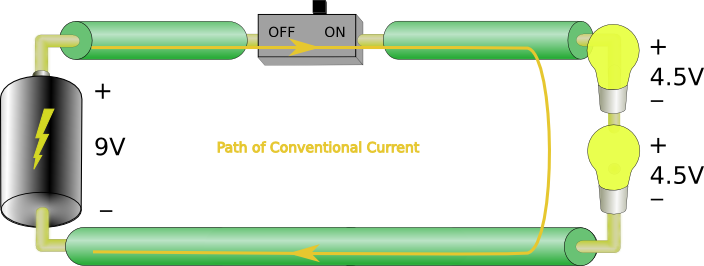
One more example to drive the point home.
This one looks a little more complex, but let’s break it down. Starting at battery BATT1’s positive terminal, we have current carriers with 9V of energy. They then move into BATT2’s negative terminal and come out of the positive terminal with an additional 3V of energy for a total of 9V+3V = 12V. Now they flow through the two lamps as in the previous example. Each lamp drops half of the 12V from the sources, 6V+6V = 12V.
Ohm’s Law: Resistance isn’t futile
Okay, Kirchoff may have had a good point, but it’s still bit academic feeling. Fortunately for us, Mr. Ohm is a bit more practical.
You may be wondering how do we know what the voltage drop will be across each load. What if we had to lamps that weren’t identical? This question was answered by Georg Ohm, as German physicist. First we need to define something called resistance. When it comes to electric current, all things will resist current flowing through them to a greater or lesser extent. Something like copper doesn’t resist current flow very well, while glass is very resistive to current. So the resistance of an object tells us how well it will or won’t pass a current. Higher resistance means it won’t pass a current well at all.
Now remember that all loads create voltage drops while current passes through them. This must mean that there is a relationship between the voltage drop and the current through the load. Mr. Ohm stated that when a load drops one volt across with one amp flowing through it we have one unit of resistance.
We call one unit of resistance an Ohm, in Mr. Ohm’s honor.
This relationship is called Ohm’s law and is described mathematically by:
Where = Ohms, V = volts and A = amps.
A couple more examples:
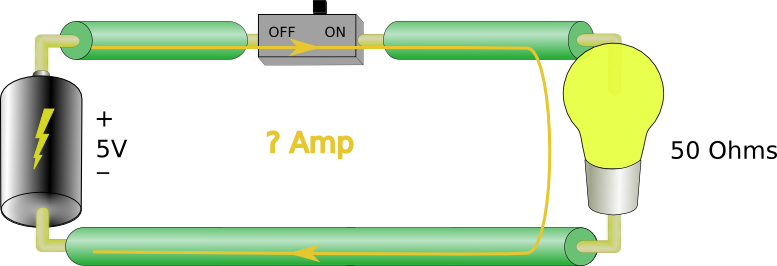
We can also rearrange the equation as follows:
So now we can find the voltage across the load if we know the current through it:
or the current in a circuit if we know the voltage and resistance
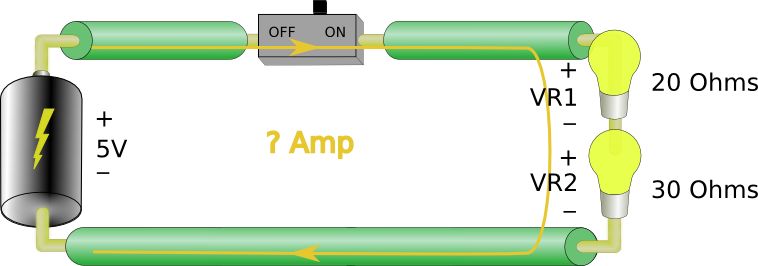
A slightly more complex example:
First we can find the total resistance of the load:
Then:
Now that we know the current in the circuit we can find VR1 and VR2:

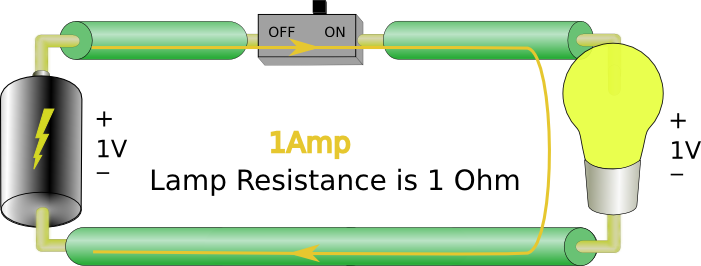
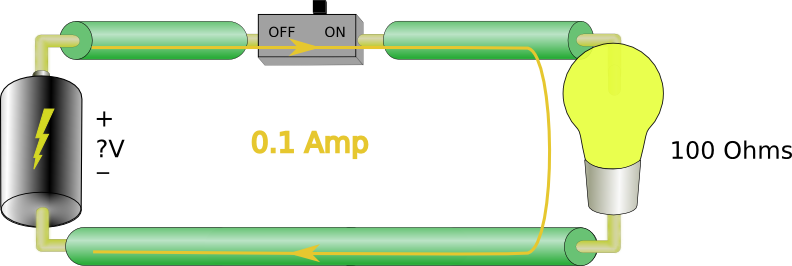
First eq. says 10 ohms = 1 V / 1 A
Thanks! Yep that is definitely a typo. Fixed now!
This site is amazing! I’ve been wanting something like this for a long time. Subscribed and eagerly awaiting new lessons. Keep up the awesome work and let me know if I can help!
Thanks!
Thanks very much
This is so good, Awesome presentation and points are explained in so cool manner.
Let me know if I can help in some Hardware tutorials.
Vr1 = 0.1A * 20 = 2.0 V
Vr2 = 0.1A * 30 = 3.0 V
——————–
Total: 5V
Please fix the typo in the image. This is a very good site and should definitely be updated. How about you make it an open source community effort for embedded devs!
Hi Rafik. Thanks for pointing that out I have updated the post. I am definitely open to making this a community effort. If you would like to contribute in any way please feel free to get in touch by email – info@simplyembedded.org. Cheers!